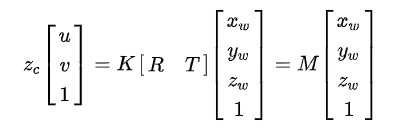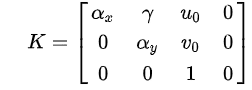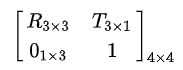La résection de la caméra est le processus d’estimation des paramètres d’un modèle de caméra à sténopé qui approxime la caméra ayant produit une photographie ou une vidéo donnée ; il détermine quel rayon lumineux entrant est associé à chaque pixel sur l’image résultante. En gros, le processus détermine la pose de la caméra à sténopé. Habituellement, les paramètres de la caméra sont représentés dans une matrice de projection 3 × 4 appelée la matrice de la caméra. Les paramètres extrinsèques définissent la pose de la caméra (position et orientation) tandis que les paramètres intrinsèques spécifient le format de l’image de la caméra (longueur focale, taille des pixels et origine de l’image).

Ce processus est souvent appelé calibration géométrique de la caméra ou simplement calibration de la caméra, bien que ce terme puisse également se référer à la calibration photométrique de la caméra ou être limité à l’estimation des paramètres intrinsèques uniquement. L’orientation extérieure et l’orientation intérieure se réfèrent respectivement à la détermination des paramètres extrinsèques et intrinsèques. La calibration classique de la caméra nécessite des objets spéciaux dans la scène, ce qui n’est pas requis dans l’auto-calibration de la caméra. La resection de la caméra est souvent utilisée dans l’application de la vision stéréo où les matrices de projection de deux caméras sont utilisées pour calculer les coordonnées mondiales en 3D d’un point vu par les deux caméras.

Avantages et inconvénients

La calibration de la caméra présente plusieurs avantages et inconvénients :

Avantages 

• La calibration aide à corriger les distorsions et les erreurs de l’image, ce qui améliore la précision de la mesure et de la localisation dans les applications de vision par ordinateur.
• Elle permet de corriger les imperfections de l’image telles que la distorsion de l’objectif, offrant ainsi des images plus nettes et plus fidèles à la réalité.
• La calibration est nécessaire dans de nombreux domaines, tels que la robotique, la navigation, la cartographie 3D, et la réalité augmentée, où la précision de la perception de l’environnement est un facteur élémentaire.
• Elle est indispensable pour la reconstruction 3D précise, permettant de créer des modèles spatiaux exacts à partir d’images 2D.

Inconvénients

• Les procédures de calibration peuvent être complexes et nécessitent une compréhension technique approfondie, ce qui peut être un défi pour les non-experts.
• Dans de nombreux cas, un équipement spécifique comme des motifs de calibration est nécessaire, ce qui peut ajouter au coût et à la complexité de la mise en place.
• Les résultats de la calibration peuvent être affectés par des facteurs environnementaux tels que l’éclairage, ce qui peut nécessiter des recalibrations fréquentes.
• Les modèles de caméra utilisés pour la calibration ne peuvent pas toujours capturer toutes les nuances réelles, ce qui peut mener à des erreurs dans certains cas.

Formule

La formulation de la matrice de projection de la caméra est dérivée des paramètres intrinsèques et extrinsèques de la caméra et est souvent représentée par une série de transformations ; par exemple, une matrice des paramètres intrinsèques de la caméra, une matrice de rotation 3 × 3, et un vecteur de translation. La matrice de projection de la caméra peut être utilisée pour associer des points dans l’espace image d’une caméra avec des emplacements dans l’espace mondial en 3D.

Coordonnées homogènes

Dans ce contexte, nous utilisons [u v 1]^T pour représenter une position de point 2D en coordonnées de pixels et [Xw Yw Zw 1]^T est utilisé pour représenter une position de point 3D en coordonnées mondiales. Dans les deux cas, ils sont représentés en coordonnées homogènes (c’est-à-dire qu’ils ont une composante supplémentaire finale, qui est initialement, par convention, un 1), ce qui est la notation la plus courante en robotique et en transformations de corps rigides.

Projection

En se référant au modèle de caméra à sténopé, une matrice de caméra M est utilisée pour désigner un mappage projectif des coordonnées mondiales aux coordonnées de pixels.

où M = K [R T]. u, v, par convention, sont les coordonnées x et y du pixel dans la caméra,

K est la matrice intrinsèque comme décrit ci-dessous, et R T forment la matrice extrinsèque comme décrit ci-dessous.

Xw, Yw, Zw sont les coordonnées de la source du rayon lumineux qui frappe le capteur de la caméra en coordonnées mondiales, par rapport à l’origine du monde. En divisant le produit matriciel par Zc, la coordonnée z de la caméra par rapport à l’origine du monde, la valeur théorique des coordonnées du pixel peut être trouvée.

Paramètres intrinsèques

La matrice K contient 5 paramètres intrinsèques du modèle spécifique de caméra. Ces paramètres englobent la longueur focale, le format du capteur d’image et le point principal de la caméra. Les paramètres α_x = f · m_x et α_y = f · m_y représentent la longueur focale en termes de pixels, où m_x et m_y sont les inverses de la largeur et de la hauteur d’un pixel sur le plan de projection et f est la longueur focale en termes de distance. [1] γ représente le coefficient de biais entre l’axe x et l’axe y, et est souvent de 0. u_0 et v_0 représentent le point principal, qui serait idéalement au centre de l’image.

Les paramètres intrinsèques non linéaires tels que la distorsion de l’objectif sont également importants bien qu’ils ne puissent pas être inclus dans le modèle de caméra linéaire décrit par la matrice des paramètres intrinsèques. De nombreux algorithmes modernes de calibration de caméra estiment également ces paramètres intrinsèques sous la forme de techniques d’optimisation non linéaires. Cela se fait sous la forme d’optimisation des paramètres de la caméra et de la distorsion sous la forme de ce qui est généralement connu sous le nom d’ajustement de faisceau.

Paramètres extrinsèques

R et T sont les paramètres extrinsèques qui dénotent les transformations du système de coordonnées de coordonnées mondiales en 3D à coordonnées de caméra en 3D. De manière équivalente, les paramètres extrinsèques définissent la position du centre de la caméra et l’orientation de la caméra dans les coordonnées mondiales.

T est la position de l’origine du système de coordonnées mondial exprimée dans les coordonnées du système de coordonnées centré sur la caméra.

T est souvent à tort considéré comme la position de la caméra. La position, C, de la caméra exprimée en coordonnées mondiales est C = –R^{-1}T = –R^TT (puisque R est une matrice de rotation).

La calibration de la caméra est souvent utilisée comme une étape préliminaire en vision par ordinateur.

Lorsqu’une caméra est utilisée, la lumière de l’environnement est focalisée sur un plan d’image et capturée. Ce processus réduit les dimensions des données prises par la caméra de trois à deux (la lumière d’une scène 3D est stockée sur une image 2D). Chaque pixel sur le plan d’image correspond donc à un faisceau de lumière de la scène originale.

Algorithmes

Il existe de nombreuses approches pour calculer les paramètres intrinsèques et extrinsèques d’une configuration de caméra spécifique. Les plus courantes sont :

• Méthode de transformation linéaire directe (DLT) : Cette méthode utilise un ensemble de points de référence dont les positions dans l’espace monde et sur l’image sont connues. En utilisant ces points, la méthode DLT résout directement les paramètres de la matrice de projection de la caméra.
• Méthode de Zhang : Une approche flexible et efficace qui ne nécessite qu’un petit nombre d’images de motifs de calibration (comme un damier) prises sous différents angles. Zhang’s method est particulièrement populaire car elle peut être mise en œuvre avec un équipement minimal et offre une bonne précision.
• Méthode de Tsai : Une méthode robuste pour la calibration de la caméra qui combine des techniques d’optimisation non linéaires et des approximations linéaires pour estimer les paramètres intrinsèques et extrinsèques.
• Méthode de Selby (pour les caméras à rayons X) : Spécialement conçue pour les caméras à rayons X, cette méthode tient compte des particularités de ces dispositifs, comme leur capacité à pénétrer les matériaux et la nature différente de leur image par rapport aux caméras traditionnelles.

Calibration de caméra et photogrammétrie

La calibration de la caméra et la photogrammétrie vont main dans la main. Lorsqu’on calibre une caméra, on ajuste et on corrige tout ce qui pourrait fausser les images, comme les distorsions de l’objectif. C’est très utile en photogrammétrie, où on a besoin que les images soient le reflet le plus fidèle de la réalité pour créer des modèles 3D précis. Sans une bonne calibration, même une petite erreur dans l’image peut se transformer en un gros problème dans le modèle final.

D’autre part, quand on travaille en photogrammétrie, on prend souvent plein d’images sous différents angles pour reconstruire un objet ou un espace en 3D. La calibration nous donne des infos clés sur où et comment chaque photo a été prise. Ça aide énormément à aligner toutes ces images ensemble correctement. C’est comme assembler un puzzle sans avoir la bonne forme des pièces – c’est là que la calibration entre en jeu pour s’assurer que tout s’emboîte parfaitement.

Calibration de caméra et géométrie épipolaire

La géométrie épipolaire et la calibration des caméras sont des composantes clés en vision stéréoscopique informatique, chacune jouant un rôle spécifique dans l’amélioration de la précision des systèmes de vision. La calibration des caméras, processus technique initial, se concentre sur l’ajustement précis des paramètres intrinsèques et extrinsèques. Cette étape corrige les distorsions optiques et assure une représentation exacte du monde capturé, établissant un cadre de référence détaillé pour chaque caméra.

Après la calibration, la géométrie épipolaire utilise ces données calibrées pour établir une relation géométrique entre les vues des caméras. Cette relation facilite la correspondance des points entre les images, essentielle pour les tâches telles que la reconstruction 3D et le suivi d’objets. Les lignes épipolaires définies par la géométrie épipolaire orientent la recherche de correspondances, simplifiant le processus de mise en correspondance.