La géométrie épipolaire est un concept fondamental en vision par ordinateur et en photogrammétrie qui décrit les propriétés géométriques et les relations entre deux vues d’une même scène prises à partir de deux positions différentes de la caméra.

Fonctionnement de la géométrie épipolaire

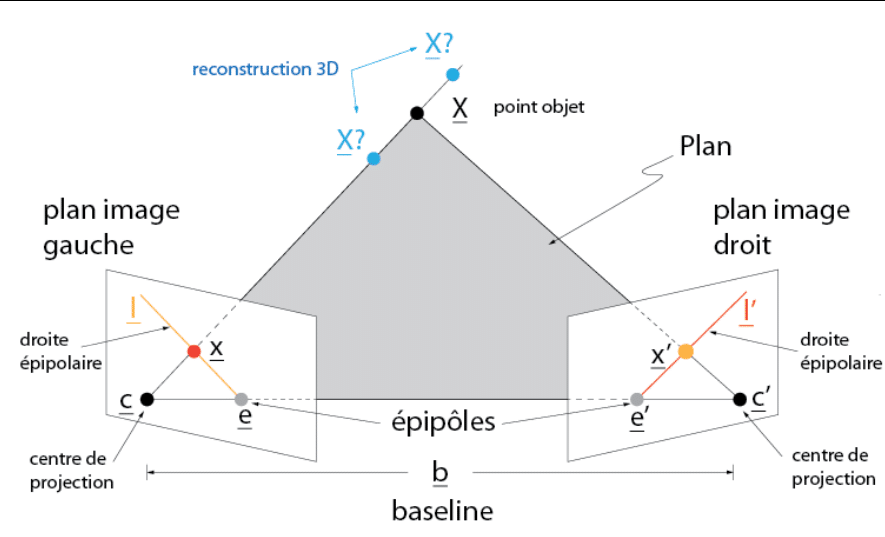
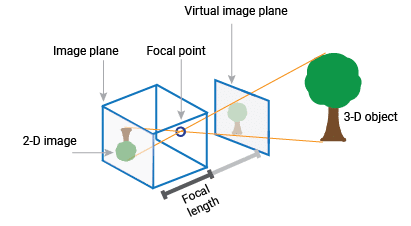
La géométrie épipolaire est utilisée en vision par ordinateur, notamment lorsqu’on travaille avec des images prises à partir de différents points de vue, un concept souvent illustré avec le modèle de la chambre à sténopé. Imaginons que vous preniez des prises de vue d’un objet depuis deux emplacements distincts. La géométrie épipolaire explore comment les points sur ces images, capturées par des caméras agissant comme des chambres à sténopé, correspondent entre eux.

Au cœur de cette géométrie se trouvent des concepts tels que les épipôles et les lignes épipolaires. Chaque prise de vue a un point appelé épipôle, qui est là où la ligne imaginaire joignant les centres optiques des deux chambres à sténopé (caméras) intersecte le plan de l’image. Si vous identifiez un point sur l’une des images, une ligne spécifique dans l’autre image, nommée ligne épipolaire, indique où le point correspondant doit se situer. Cela simplifie la recherche du point correspondant dans la seconde image, la limitant à cette ligne plutôt qu’à l’ensemble de l’image.

Il y a également la contrainte épipolaire : si un point dans l’espace est capturé dans les deux prises de vue, alors les images de ce point, combinées aux positions des deux chambres à sténopé, doivent toutes résider sur un même plan.

Pour quantifier ces relations, des matrices comme la matrice fondamentale ou la matrice essentielle sont employées. Ces matrices sont fondamentales pour décrire les relations géométriques dans les systèmes de chambre à sténopé, que les caméras soient calibrées ou non.

Dans la pratique, la géométrie épipolaire est cruciale pour des applications telles que la reconstruction 3D d’une scène à partir de multiples prises de vue, l’alignement et la calibration des caméras, et la stéréovision, où l’objectif est de comprendre la profondeur et la structure d’une scène à partir de deux images. En somme, elle facilite grandement la tâche de mise en correspondance des points entre différentes images, rendant le processus beaucoup plus intuitif et gérable.

Applications

Reconstruction 3D

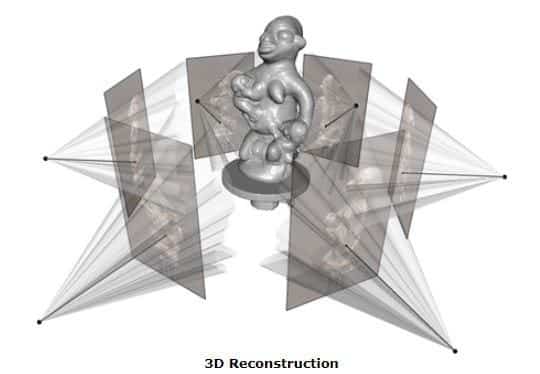
La reconstruction 3D est l’une des applications majeures de la géométrie épipolaire. Elle permet de créer des modèles tridimensionnels précis à partir de plusieurs images bidimensionnelles. Cette technique est largement utilisée dans des domaines variés, allant de l’architecture à la robotique, en passant par les jeux vidéo et le cinéma. Grâce à la géométrie épipolaire, il est possible de déterminer avec précision la position et l’orientation des objets dans l’espace, ce qui est essentiel pour générer des modèles 3D réalistes et précis.

En outre, la reconstruction 3D joue un rôle crucial dans l’industrie de la conception assistée par ordinateur (CAO) et dans les études archéologiques. Les architectes et les ingénieurs utilisent ces modèles pour visualiser les projets avant leur construction, tandis que les archéologues peuvent reconstruire des sites ou des artefacts endommagés. La géométrie épipolaire aide à fusionner différentes vues de l’objet pour créer une représentation complète et détaillée.

Stéréovision

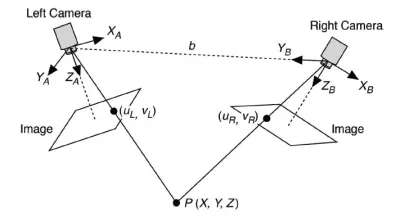
La stéréovision, inspirée de la vision binoculaire humaine, est une autre application clé de la géométrie épipolaire. Dans ce système, deux caméras capturent la même scène sous des angles différents (principe de la mesure stéréoscopique), permettant de calculer la profondeur et la distance des objets. Cette technologie est fondamentale dans des domaines comme l’automobile pour les voitures autonomes, où la détection précise des obstacles est cruciale pour la sécurité.

La stéréovision est également utilisée dans la recherche scientifique, notamment en biologie et en physique, pour mesurer les mouvements et les distances dans des environnements complexes. En analysant comment les points se correspondent entre les deux images, il est possible de créer une carte de profondeur détaillée de la scène observée, offrant ainsi une compréhension plus profonde de l’espace tridimensionnel.

Calibration de caméras

La calibration de caméras est une autre application importante de la géométrie épipolaire. Cette procédure permet de déterminer les paramètres internes et externes des caméras, tels que la position, l’orientation et la focale. Cette étape est essentielle pour garantir la précision dans des applications comme la modélisation 3D, la robotique et la télédétection.

Dans les systèmes de vision industrielle, la calibration des caméras est cruciale pour assurer la précision des mesures et la qualité des inspections. Elle permet aux systèmes automatisés de comprendre leur environnement, d’effectuer des tâches de manipulation précises et de détecter des défauts dans les processus de fabrication.

Navigation et cartographie

La géométrie épipolaire est fondamentale dans la navigation et la cartographie, en particulier pour les véhicules autonomes et les drones. Elle permet de cartographier l’environnement et de naviguer en détectant et en mesurant la position des objets. Cette technologie est essentielle pour permettre aux systèmes autonomes de se déplacer en toute sécurité et efficacement dans des environnements complexes.

Dans le domaine de la géographie et de la planification urbaine, la géométrie épipolaire aide à créer des cartes détaillées et à jour. Elle est également utilisée dans les systèmes de cartographie pour les applications de réalité augmentée, où il est nécessaire de superposer des informations virtuelles sur des images du monde réel.

Réalité augmentée et virtuelle

Dans les domaines de la réalité augmentée (RA) et de la réalité virtuelle (RV), la géométrie épipolaire joue un rôle crucial pour assurer un alignement précis entre les objets virtuels et réels. Elle aide à comprendre la perspective et l’orientation de l’utilisateur dans l’espace, ce qui est essentiel pour créer une expérience immersive et crédible.

En RA, par exemple, la géométrie épipolaire est utilisée pour superposer des informations ou des objets virtuels sur des images du monde réel de manière précise. En RV, elle aide à créer des environnements tridimensionnels dans lesquels les utilisateurs peuvent interagir de manière naturelle, améliorant ainsi l’expérience